Rather than fully bake this idea before writing up a post on it (not that anyone reads this stuff but me anyhow) I thought I would experiment with writing as I think with minimal retroactive edits, so let’s see how this goes!
I am playing with the point of view that all integers can be thought of as the volume of a unique n dimensional hypercube. I would like to look at this in a way where these hypercubes don’t simply exist for each integer, but that the definition of what an integer is arises from the natural existence of these unique geometric hypercube configurations.
I start with defining a unit hypercube, infinite in dimensions and with each of those dimensions measuring a length of 1 resulting in a volume of 1. Or said another way so as to avoid defining a word using that word, the length of each side is simply of the same length and we will define the resulting volume, lengths and proportions of the dimensions as what the integer “1” means. I also hold that the harmonic actions of doubling, tripling, etc are concepts that can be applied without it being a recursive definition. For brevity I will refer to this infinite unit hypercube as simply a unit-cube.
I like to whimsically imagine this unit-cube as the most fundamental 1-pip lego building block that hyperdimensional alien children build their celestial temples with
Now if we stack one of these identity hypercubes on top of another, or equivalently, stretch one so that one dimension is double that of the others, then we have through its volume defined the number 2.
We could also arrive at 2 by stretching the identity hypercube in more than one dimension by amounts that are not in increments of the unit size, for instance we could reduce one dimension by one half and another we could quadruple [0.5 x 4 x 1 x 1 x 1… = 2] or we could also arrive at a volume of 2 by setting three dimensions to the cube root of 2 [1.25… x 1.25… x 1.25… x 1 x 1 x 1… = 2]. In fact there are obviously an infinite number of ways we could size an infinite hypercube to have a volume of 2. So let us simply make the rule that the dimensions must be multiples of the unit length.
As an alternative rule to address fractional dimensions we could focus on the fact that the relationship between the dimensions are what define them and abandon the precept of any absolute lengths. That is to say, [0.5 x 4 x 1 x 1 x 1… = 2] is more appropriately defined as the proper ratios to a unit length [1 x 8 x 2 x 2 x 2… = Infinity].
Yet another thought for fractional dimensional lengths are to treat them as a folding space into a special anti-dimension. I for instance I can feel my way through the 1/2 dimension in the example above [0.5 x 4 x 1 x 1 x 1… = 2] as the numerator staying as a positive dimension and the denominator as new kind of anti-dimension, one that doesn’t expand the space into a new direction but folds it, perhaps a corollary to an imaginary number such that that example should be expressed in a more complex form [4x1x1x1… + 2x1x1x1…i]. It is actually a neat association but the impact of increasing an imaginary component has a trigonometric (and not fractional) impact on the real component so far from equivalent…. something to ponder another time…
When we try to define 3 we recognize that stacking and stretching are not synonymous. If we are stacking unit-cubes we could stack them three high or also could stack them two high and place one beside the first. Let us clarify our process going forward to be the stretching and not stacking. That being the case, there is only one way to stretch a unit-cube to the volume of three while maintaining rational dimensional lengths equal to or greater than 1; That is simply [3 x 1 x 1 x 1…. = 3].
To define 4, we now recognize that there is more than one way to define a valid hypercube even with stretching; in this instance [4 x 1 x 1 x 1… = 4] and [2 x 2 x 1 x 1 x 1… = 4]. At this point we arrive at what will be the primary rule, and that is that the cube must be the most compact cube possible. But what does this mean? At this point I cannot definitively claim to have the ‘right’ test. The infinite dimensions prevent easily measuring these cubes because any measurement that isn’t parallel to a dimension is infinite in length. A formal definition is perhaps not required at this stage as a casual observation is that any dimensional length that can instead be represented by a larger quantity of smaller dimensions naturally makes for a more compact representation; [2 x 2 x 1 x 1 x 1… = 4] is clearly more compact than [4 x 1 x 1 x 1… = 4] as [4] can be represented in the more compact form of [2 x 2].
Now having danced around what is likely very obvious at this time, let us speak plainly that the dimensions of these hypercubes are simply the prime factorizations of their volumes. A prime number then is a unit-cube that is stretched in a single dimension because there is no rational harmonic that can be folded into another dimension.
Now let’s think about roots in this geometric fashion. Interestingly it becomes about dividing a cube into identical sub cubes. This in practice is more of a combinatorics problem looking for how its dimensions can be grouped by the radical.
- 25 [5 x 5 x 1…] -Square Root-> 5 [5 x 1…]
- 8 [2 x 2 x 2 x 1…] -Cube Root-> 2 [2 x 1…]
- 36 [2 x 2 x 3 x 3 x 1…] -Square Root-> 6 [2 x 3 x 1 x 1…]
- 1,838,265,625 [ 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 1…] -Sixth Root-> 35 [5 x 7 x 1…]
- 1,838,265,625 [ 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 1…] -Square Root-> 42,875 [5 x 7 x 5 x 7 x 5 x 7 x 1…]
- 42,875 [5 x 7 x 5 x 7 x 5 x 7 x 1…] -Cube Root-> 35 [5 x 7 x 1…]
If there is no way to subdivide the cube into the radical, then the resultant cube consists of sides that are not harmonic multiples of the unit-cube and thus by definition is an irrational number. 25 [5 x 5 x 1…] -Cube Root-> ~2.92 [~2.92 x 1…]
Multiplication of cubes we then are implicitly defining as a process where the resultant cube contains each of the dimensions of the two multiplying cubes. This can be thought of as the dimensions of the first cube scaling their associated discreet dimensions in the second cube and if necessary factoring back down to the most compact form.
As Multiplication feels more like adding dimensions, Division is more akin to removing them wherein the dimensions of the denominator are removed from the numerator:
- 25 [5 x 5 x 1…] / 5 [5 x 1…] = 5 [5 x 1…]
- 8 [2 x 2 x 2 x 1…] /4 [2 x 2 x 1…] = 2 [2 x 1…]
- 1,838,265,625 [ 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 1…] / 35 [5 x 7 x 1…] = 52,521,875 [ 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 5 x 7 x 1…]
If the dimensions of the denominator do not exist in the numerator then the resultant cube is fractional. Earlier on I deferred truly delving into fractional dimensions so I am going to hold on that here as well until I come back through on that topic. There is also an inherent linear algebraic feel to this with even the multidimensional cube arguably being nothing more than a transformation matrix so I am also tabling thinking about the corollaries of dot and cross product operations as well.
Next I want to consider addition. I want to start by thinking about how a number is defined by the sum of two numbers and contrast that with whether we can subdivide its cube to arrive at those two sub cube or take two cubes and stack them to the cube of the sum. Let’s start with a simple one that we can visualize, 9 [3 x 3 x 1…]:
- 1 [1 x 1…] + 8 [2 x 2 x 2 x 1…]
- 2 [2 x 1…] + 7 [7 x 1…]
- 3 [3 x 1…] + 6 [3 x 2 x 1…]
- 4 [2 x 2 x 1…] + 5 [5 x 1…]
So as we look at that, we realize that only in the case of 3 + 6 can we consider addition truly the “stacking” of two cubes to result in the geometry of the 9 cube. What does this mean? Let’s try another example and see if we can generalize something from this, let’s use something larger: 42 [7 x 3 x 2 x 1…]
- 1 [1 x 1…] + 41 [41 x 1…]
- 2 [2 x 1…] + 40 [5 x 2 x 2 x 2 x 1…]
- 3 [3 x 1…] + 39 [13 x 3 x 1…]
- 4 [2 x 2 x 1…] + 38 [19 x 2 x 1…]
- 5 [5 x 1…] + 37 [37 x 1….]
- 6 [2 x 3 x 1…] + 36 [3 x 3 x 2 x 2 x 1…]
- 7 [7 x 1…] + 35 [7 x 5 x 1…]
- 8 [2 x 2 x 2 x 1…] + 34 [17 x 2 x 1…]
- 9 [3 x 3 x 1…] + 33 [11 x 3 x 1…]
- 10 [5 x 2 x 1…] + 32 [2 x 2 x 2 x 2 x 2 x 1…]
- 11 [11 x 1…] + 31 [31 x 1…]
- 12 [3 x 2 x 2 x 1…] + 30 [5 x 3 x 2 x 1…]
- 13 [13 x 1…] + 29 [29 x 1…]
- 14 [7 x 2 x 1…] + 28 [7 x 2 x 2 x 1…]
- 15 [5 x 3 x 1…] + 27 [3 x 3 x 3 x 1…]
- 16 [2 x 2 x 2 x 2 x 1…] + 26 [13 x 2 x 1…]
- 17 [17 x 1…] + 25 [5 x 5 x 1…]
- 18 [3 x 3 x 2 x 1…] + 24 [3 x 2 x 2 x 2 x 1…]
- 19 [19 x 1…] + 23 [ 23 x 1…]
- 20 [5 x 2 x 2 x 1…] + 22 [11 x 2 x 1…]
- 21 [7 x 3 x 1…] + 21 [7 x 3 x 1…]
In this larger set we can see three pairs that can be stacked to the geometry of a 42 cube. What we notice in this exercise is what stacking really means; it is the extension of a cube in a single dimension. This implies that other than the dimension of the extension, the other dimensions must be identical. So 42 [7 x 3 x 2 x 1…] can be stacked up to in one of three ways:
- [A x 3 x 2 x 1…] + [B x 3 x 2 x 1…] where A + B = 7
- [7 x A x 2 x 1…] + [7 x B x 2 x 1…] where A + B = 3
- [7 x 3 x A x 1…] + [7 x 3 x B x 1…] where A + B = 2
Furthermore, A and B must be prime. So that gets us the satisfying answers above as follows:
- [A x 3 x 2 x 1…] + [B x 3 x 2 x 1…] where A + B = 7
- 12 [2 x 3 x 2 x 1…] + 30 [5 x 3 x 2 x 1…] where 5 + 2 = 7
- [7 x A x 2 x 1…] + [7 x B x 2 x 1…] where A + B = 3
- 14 [7 x 2 x 1…] + 28 [7 x 2 x 2 x 1…] where 1 + 2 = 3
- [7 x 3 x A x 1…] + [7 x 3 x B x 1…] where A + B = 2
- 21 [7 x 3 x 1…] + 21 [7 x 3 x 1…] where 1 + 1 = 2
When we look at it like that it is clear that is is the exhaustive list of solutions and it is a generalized approach to solving that can be applied for any number. But what about the other addition solutions, how do we account for them; is this a special operation distinct from Addition? And what can we learn from looking at the addition of more than simply 2 numbers?
Well if we experiment with 15 [5 x 3 x 1…] + 27 [3 x 3 x 3 x 1…] = 42 [7 x 3 x 2 x 1…] we can visualize this as three 3D blocks: 5x3x1, 3x3x3 and 7x3x2. Now we can start to think of how we could cut those first two blocks up and reassemble them to make the latter. So here is one approach to accomplish this represented graphicaly:
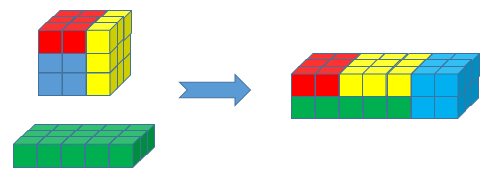
And here it is as a flow chart:

As is best illustrated by the graphical representation, the subdivision of 27 results in 3 cubes that are all properly defined in their most compact form; Later I illustrate violating this rule. As you can see in the flow representation, each step of the construction is properly defined as stacking in a single dimension; Later I illustrate constructions that seem valid but break this rule. What I find fascinating about this is that the geometry of cutting up the block using your visual intuition is supported by the math of breaking down and stacking blocks in such a way that they satisfy the observation previously of blocks sharing all but one common dimension. That is to say we could have solved this solely through the mathematical gyrations illustrated in the flow, entirely agnostic of the tangible geometric sense of cutting and stacking blocks together!
Can every addition be satisfied by this method? Yes, certainly you could devolve each block down to all individual unit-cubes and build it back up. How many ways can we solve these addition problems? How can we devise an algorithm to determine the most efficient way?
Let’s setup some problems to violate the two rules we followed above. First let’s look at what happens when we violate the most-compact-cube rule by addition and subdvision. First there is the condition in this example: 4 [2x2x1…] + 4 [2x2x1…] going to the uncompacted form 8 [4x2x1…] instead of 8 [2x2x2x1…]. Geometrically this is equivalent to stacking compatible dimensions but building an invalid structure as below:
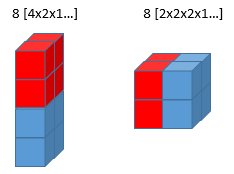
Second there is the related converse condition in this example: 11 [11×1…] subdividing into [3×1…] + and the uncompacted form 8 [8×1…] instead of 8 [2x2x2x1…]. Geometrically this is equivalent to properly subdividing a block but again into an invalid structure.
I assert that both these additions and subdivisions into uncompacted structures are violations of the addition process I am attempting to define. I might like to consider allowing for uncompacted structures to be generated by addition and subdivision provided they are immediately compressed to their proper form. Here is an an example of a construction using that approach to consider. Here we are adding 11 [11×1…] + 7 [7×1…] to get 18 [3x3x2x1…]. As you can see we subdivide the 7 to 4 (blue) and 11 to 8 (green), both of which must immediately compact before they can be stacked. I am open to this approach; the alternative would be to subdivide by 3s, stack the remaining 2 and 1 to another 3 and stack all 3s to make the 18.
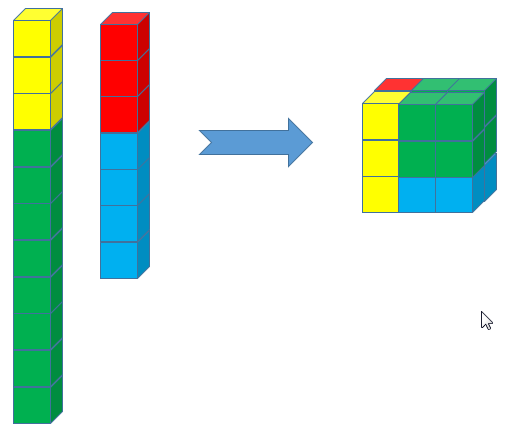

Now let’s look at a neat construction of a valid cube from valid subcubes but through a flow that cannot be accomplished through individual additions/subdivisions. 2 [2×1…] + 2 [2×1…] + 2 [2×1…] + 2 [2×1…] + 1 [1×1…] = 9 [3x3x1…]. As you can see below, you cannot stack or unstack (subdivide) this one step at a time per the rules previously laid out because you would need to stack/subdivide them simultaneously. Is this a valid construction? If so, I may need to redefine stacking which I described as the constraining a single dimension. This seems as though it would be difficult to arrive at this construction agnostic the geometry.

So at this point we have defined roots, multiplication, division, addition (and implicitly subtraction) through construction and by necessity subdivision. What’s next? Well we shall see when (if?) I feel like coming back and adding to!
Reminder when I come back:
I was thinking a little bit about the ABC Conjecture and considering it in the context of this. The conjecture starts with the definition of a radical, and in this case I would state it as being the product of the distinct dimensions of the cube where distinct means in magnitude. So what does that mean geometrically? Here are some examples they provide, let’s consider them:
- rad(16) = rad(24) = 2
- rad(17) = 17
- rad(18) = rad(2 ⋅ 32) = 2 · 3 = 6
- rad(1000000) = rad(26 ⋅ 56) = 2 ⋅ 5 = 10
Well the first thing I notice is that if the exponents of the factors are the same then the result is equivalent to simply taking the maximum root of the number; it is effectively the maximum root of each factor. A geometric animation for this in my head is divide (as in division, not separation) the cube into discreet