Infrequently I stay in Manhattan for work. On one occasion I ended up staying quite some distance away from the office to save the company some money but I still opted to walk in. Along the way I came to think that there is a certain potential efficiency to traveling between two points in the city that are diagonal from one another; that is to say where you are not on the same street. This is because at each intersection if you are met with a do not walk in one direction you can travel in the other and still progress towards your destination. If you were the same number of blocks away but on the same street you would have no choice but to wait for each crossing you encounter such that each linear block you are forced to travel you have a 50% chance of adding a wait time to your total walk time. I decided to study this a little further and build an interactive simulator to heat map travel times on a grid.
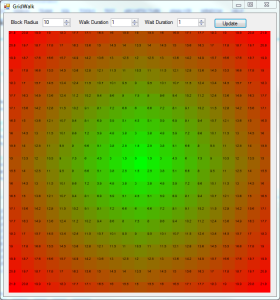
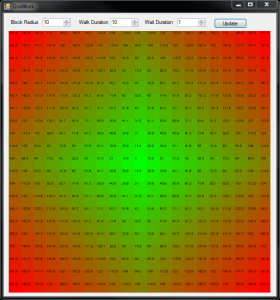
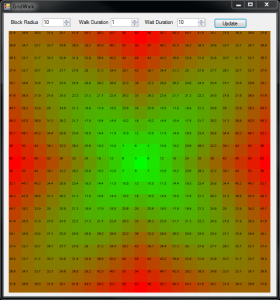
Below is a screenshot of the interface where you can see two controls at the top that allow you to change the time it takes to walk a block and the average time you would wait at an intersection to cross. Below those controls is a visualization of the resultant walk times where the center block in the grid represents your destination and every other block on the grid is a potential starting point. The heat map is blended from green for short travel times to red for long travel times and is based on, as well as displays within it, the average travel time.
I think the visualization helps you to appreciate the shift in geometry of a high vs low walk-to-wait time ratios as the contours of the heat map morphs from a circle to a square to a star. Walk time indicates the time it takes to walk a block and Wait time indicates how long it takes to wait for a light to cross.
Left: walk time = wait time. Center: walk time > wait time. Right: walk time < wait time
If I were to explore further I would next take a more probabilistic tact as the averages are insightful but as a risk taker I would like to better understand the probability of a longer diagonal path with a higher average walk time still being faster than a linear path. I might code for the selection of two starting points with a readout on the probability that you would arrive faster from one vs the other.