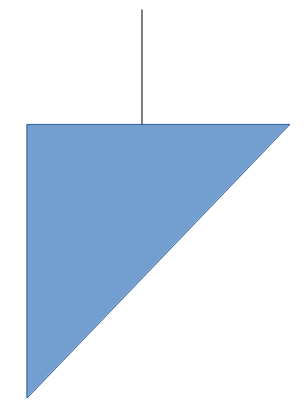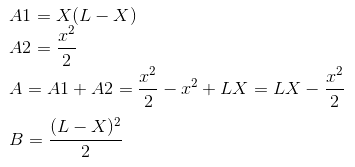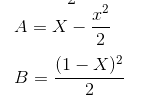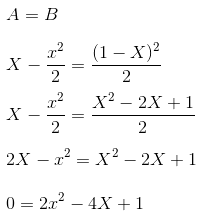I recall I was taking a shower and was thinking about the mathematics of mobiles, something for another post, but during this I got to thinking about how to generalize a formula for finding the point to balance a triangle such that it would hang like this:
I sorted most of it out in my head and then scribbled down the rest over breakfast. I just found that scrap of paper years later and thought I would transcribe it!
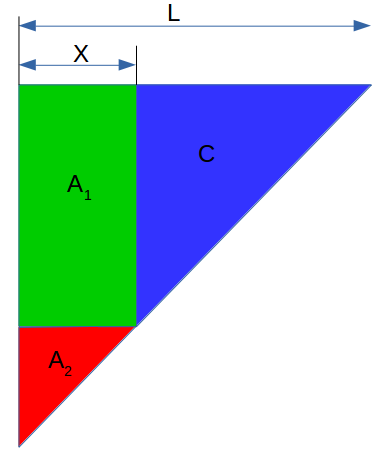
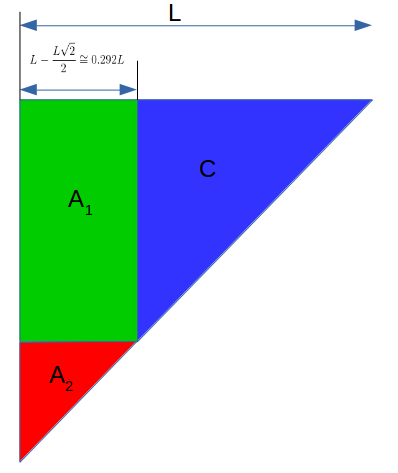
The way I reasoned this was to come up with a formula to determine the area of a triangle to the left of the hanging point and to the right, I did that like this where the balancing point is at X such that the areas of A1 + A2 = B and we are looking solve for X as a proportion of L.
So we define the areas of A and B with respect to L and X as follows:
But knowing that we are looking for only the proportion between L and X we can simply set L to 1 and then X will represent the proportion all by itself:
And now we set A and B equal to each other and come out with a quadratic equation:
We quickly look up the formula for the quadratic equation that you thought you would never need and substitute in:
1.707 doesn’t make sense so it is the latter 0.292, giving us our answer! So to find the distance to balance a triangle attach the line to a point 1 – sqrt(2)/2 times the length of the side!
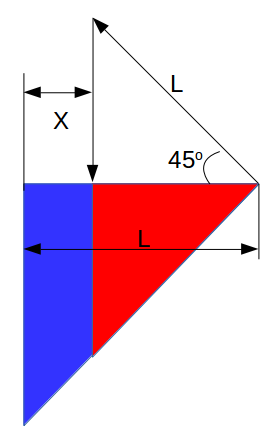
But wait! There is a really interesting construction method I wrote down as well. I am really not sure how I spotted this but it is super sexy! As you can see below, you can also find the balancing point X quite easily by rotating the length 45 degrees off the triangle and projecting a line back down!